Spelling with Elemental Symbols
(Full source code is available here.)
Sitting in my 5-hour-long chemistry class, my gaze would often drift over to the periodic table posted on the wall. To pass the time, I began to try finding words I could spell using only the symbols of the elements on the periodic table. Some examples: ScAlEs, FeArS, ErAsURe, WAsTe, PoInTlEsSnEsS, MoISTeN, SAlMoN, PuFFInEsS.
I wondered what the longest such word was ('TiNTiNNaBULaTiONS' was the longest one I could come up with). Then I started thinking about how nice it would be to have a tool that could find the elemental spellings of any word. I decided to write a Python program. Given a word as input, it would output all elemental spellings for that word:
- Input:
- 'Amputations'
- Output:
- 'AmPuTaTiONS', 'AmPUTaTiONS'
Generating Character Groupings
If all the symbols of all the elements were the same length, the task would be trivial. However some elemental symbols are glyphs consisting of two characters ('He'), while others are single-character glyphs ('O'). This turns out to make things much more complex. The 'pu' in 'Amputations' can be represented either by Plutonium ('Pu') or by Phosphorus and Uranium ('PU'). Any given word would need to be broken down into all possible combinations of single and double-character glyphs.
I decided to call each of these permutations a 'grouping'. Groupings specify the division of a word into glyphs. A grouping can be represented as a tuple of 1s and 2s where 1 represents a single character glyph and 2 represents a double character glyph. Every elemental spelling corresponds to some grouping:
- 'AmPuTaTiONS'
(2,2,2,2,1,1,1)
- 'AmPUTaTiONS'
(2,1,1,2,2,1,1,1)
In an attempt to explore the problem and find patterns, I wrote the following table in my notebook:
Question: For a string of length n, how many sequences of 1s and 2s exist such that the sum equals n?
| n | # Groupings | Groupings |
|---|---|---|
| 0 | 1 | () |
| 1 | 1 | (1) |
| 2 | 2 | (1,1), (2) |
| 3 | 3 | (1,1,1), (2,1), (1,2) |
| 4 | 5 | (1,1,1,1), (2,1,1), (1,2,1), (1,1,2), (2,2) |
| 5 | 8 | (1,1,1,1,1), (2,1,1,1), (1,2,1,1), (1,1,2,1), (1,1,1,2), (2,2,1), (2,1,2), (1,2,2) |
| 6 | 13 | (1,1,1,1,1,1), (2,1,1,1,1), (1,2,1,1,1), (1,1,2,1,1), (1,1,1,2,1), (1,1,1,1,2), (2,2,1,1), (2,1,2,1), (2,1,1,2), (1,2,2,1), (1,2,1,2), (1,1,2,2), (2,2,2) |
| 7 | 21 | (1,1,1,1,1,1,1), (2,1,1,1,1,1), (1,2,1,1,1,1), (1,1,2,1,1,1), (1,1,1,2,1,1), (1,1,1,1,2,1), (1,1,1,1,1,2), (2,2,1,1,1), (2,1,2,1,1), (2,1,1,2,1), (2,1,1,1,2), (1,2,2,1,1), (1,2,1,2,1), (1,2,1,1,2), (1,1,2,2,1), (1,1,2,1,2), (1,1,1,2,2), (2,2,2,1), (2,2,1,2), (2,1,2,2), (1,2,2,2) |
Answer:
fib(n + 1)!?
I was surprised to find the Fibonacci sequence in this unexpected place. During my subsequent investigations, I was even more surprised to discover that knowledge of this particular pattern goes back almost 2000 years to the prosodists of ancient India, who discovered it in their study of the permutations of short and long syllables of Vedic chants. For a fascinating exploration of this and other advancements in the history of combinatorics, consult section 7.2.1.7 of The Art of Computer Programming by Donald Knuth.
Fascinating as this finding was, I still hadn't accomplished my actual goal: To generate the groupings themselves. Some pondering and experimentation led me to the most straightforward solution I could think of: to generate all possible sequences of 1s and 2s, then filter out any that don't sum to the length of the input word.
from itertools import chain, product
def generate_groupings(word_length, glyph_sizes=(1, 2)):
cartesian_products = (
product(glyph_sizes, repeat=r)
for r in range(1, word_length + 1)
)
# include only groupings that represent the correct number of chars
groupings = tuple(
grouping
for grouping in chain.from_iterable(cartesian_products)
if sum(grouping) == word_length
)
return groupings
A Cartesian product is the set of all tuples composed of a given set of
elements. The Python Standard Library provides itertools.product(),
a function that returns the Cartesian product of the elements in a given
iterable. cartesian_products is a generator expression that yields every
possible permutation of the items in glyph_sizes up to the given length,
word_length.
So, if word_length is 3, cartesian_products will yield:
[
(1,), (2,), (1, 1), (1, 2), (2, 1), (2, 2), (1, 1, 1), (1, 1, 2),
(1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2)
]
These are then filtered so that groupings ends up only including those
permutations whose elements add up to word_length.
>>> generate_groupings(3)
((1, 2), (2, 1), (1, 1, 1))
Clearly, there is a lot of extra work being done here. The function calculated
14 permutations, but only ended up using 3. The performance gets rapidly worse
as word_length increases. More on that later. Having gotten this function
working, I moved on to the next task.
Mapping Words to Groupings
Once all the possible groupings for a word have been calculated, that word can be "mapped" to each grouping:
def map_word(word, grouping):
chars = (c for c in word)
mapped = []
for glyph_size in grouping:
glyph = ""
for _ in range(glyph_size):
glyph += next(chars)
mapped.append(glyph)
return tuple(mapped)
The function treats each glyph in the grouping like a cup, and fills it with as many characters from the word as it can hold before moving on to the next one. When all the characters have been placed in the proper glyph, resulting mapped word is returned as a tuple.
>>> map_word('because', (1, 2, 1, 1, 2))
('b', 'ec', 'a', 'u', 'se')
Once a word is mapped, it's ready to be compared to the list of elemental symbols to find any possible spellings.
Finding the Spellings
With the other two functions doing most of the work, I made a spell() function
which tied everything together:
def spell(word, symbols=ELEMENTS):
groupings = generate_groupings(len(word))
spellings = [map_word(word, grouping) for grouping in groupings]
elemental_spellings = [
tuple(token.capitalize() for token in spelling)
for spelling in spellings
if set(s.lower() for s in spelling) <= set(s.lower() for s in symbols)
]
return elemental_spellings
spell() gets all possible spellings, returning only those that are entirely
composed of elemental symbols. I used sets to efficiently filter out any invalid
spellings.
Python's sets are are very similar to mathematical sets. They are unordered
collections of unique elements. Behind the scenes, they are implemented as
dictionaries (hash-tables) with keys, but no values. Since all the elements in
a set are hashable, membership tests are very efficient (average case O(1)
time). The comparison operators are overloaded to test for subsets by
using these efficient membership operations. Sets and dictionaries are deeply
explored in the wonderfully informative book, Fluent Python by Luciano
Ramalho.
With this last component functional, I finally had a working program!
>>> spell('amputation')
[('Am', 'Pu', 'Ta', 'Ti', 'O', 'N'), ('Am', 'P', 'U', 'Ta', 'Ti', 'O', 'N')]
>>> spell('cryptographer')
[('Cr', 'Y', 'Pt', 'Og', 'Ra', 'P', 'H', 'Er')]
The Longest Word?
Happy to have implemented the core functionality, I gave my program a name (Stoichiograph), and made a command line wrapper for it. The wrapper takes words, either as arguments or from a file, and prints out their spellings. After adding an option to order the words descendingly by length, I let my program loose on my unsuspecting list of words.
$ ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
NoNRePReSeNTaTiONaL
NoNRePReSeNTaTiONAl
[...]
Nice! That definitely wasn't a word I would have ever thought of myself. My program was already fulfilling its purpose. I played around a bit and found a longer word:
$ ./stoichiograph.py nonrepresentationalisms
NoNRePReSeNTaTiONaLiSmS
NONRePReSeNTaTiONaLiSmS
NoNRePReSeNTaTiONAlISmS
NONRePReSeNTaTiONAlISmS
Interesting. I wondered whether this was truly the longest word (spoiler), and I wanted to investigate longer words. First, though, I needed to make my program run much faster.
Addressing Performance Issues
It took my program about 16 minutes to work through the 119,095 words (of which many were quite short) in my word list:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
[...]
real 16m0.458s
user 15m33.680s
sys 0m23.173s
That's about 120 words per second on average. I was sure I could make it faster. I needed more detailed performance information to know how best to do so.
Line profiler is a tool for identifying performance bottlenecks in Python code. I used it to profile my program as it found spellings for a single 23-character-long word. Here's a condensed version of what it had to say:
Line # % Time Line Contents
===============================
30 @profile
31 def spell(word, symbols=ELEMENTS):
32 71.0 groupings = generate_groupings(len(word))
33
34 15.2 spellings = [map_word(word, grouping) for grouping in groupings]
35
36 elemental_spellings = [
37 0.0 tuple(token.capitalize() for token in spelling)
38 13.8 for spelling in spellings
39 if set(s.lower() for s in spelling) <= set(s.lower() for s in symbols)
40 ]
41
42 0.0 return elemental_spellings
Line # % Time Line Contents
===============================
45 @profile
46 def generate_groupings(word_length, glyhp_sizes=(1, 2)):
47 cartesian_products = (
48 0.0 product(glyph_sizes, repeat=r)
49 0.0 for r in range(1, word_length + 1)
50 )
51
52 0.0 groupings = tuple(
53 0.0 grouping
54 100.0 for grouping in chain.from_iterable(cartesian_products)
55 if sum(grouping) == word_length
56 )
57
58 0.0 return groupings
It is not a great surprise that generate_groupings() takes so long. The
problem it tries to solve is a special case of the subset sum problem
which is NP-complete. Finding a cartesian product gets expensive quickly,
and generate_groupings() finds multiple cartesian products.
We can perform asymptotic analysis to get a sense of just how horrifically bad things are:
- We assume that
glyph_sizesalways has 2 elements (1 and 2). product()finds the cartesian product of a set of 2 elementsrtimes, so the big O ofproduct()isO(2^r).product()is called in a for loop which repeatsword_lengthtimes, so if we setnasword_length, the big O for the whole loop isO(2^r * n).- But
rhas a different value each time the loop runs, so really it's more likeO(2^1 + 2^2 + 2^3 + ... + 2^(n-1) + 2^n). - And since
2^0 + 2^1 + ... + 2^n = 2^(n+1) - 1, our final big O is:O(2^(n+1) - 1), orO(2^n).
With O(2^n) time complexity we can expect the execution time to double for
each incrementation of word_length. Horrifying!
I thought about this performance problem for many weeks. I had two related, but distinct, performance cases to consider:
- Processing a list of words of varying length.
- Processing a single, but very long word.
The second case proved, as one might guess, to be much more important because it affected the first. Though I didn't immediately know how to improve case 2, I had some ideas for case 1, so that's where I started.
Case 1: Being Lazy
Laziness is a virtue not only for programmers, but also for programs themselves. Addressing case 1 required laziness. If my program was going to process a long list of words, how could I get my program to do as little work as possible?
Checking for Invalid Characters
Surely, I thought, there are likely to be words in a given list that contain characters not present in any elemental symbol. Time expended trying to find spellings for these words is time wasted. A word list could be processed faster if these words were quickly identified and skipped.
Unfortunately for me, it turns out that 'j' and 'q' are the only letters not contained in any elemental symbol:
>>> set('abcdefghijklmnopqrstuvwxyz') - set(''.join(ELEMENTS).lower())
('j', 'q')
And only about 3% of the words in my particular dictionary file contain 'j' or 'q':
>>> with open('/usr/share/dict/american-english', 'r') as f:
... words = f.readlines()
...
>>> total = len(words)
>>> invalid_char_words = len(
... [w for w in words if 'j' in w.lower() or 'q' in w.lower()]
... )
...
>>> invalid_char_words / total * 100
3.3762962340988287
Skipping those words made the program only about 2% faster:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
[...]
real 15m44.246s
user 15m17.557s
sys 0m22.980s
Not the kind of performance improvement I was hoping for, so on to the next idea.
Memoization
Memoization is the technique of saving a function's output and returning it if the function is called again with the same inputs. A memoized function only needs to generate output once for a given input. This can be very helpful with expensive functions that are called many times with the same few inputs, but only works for pure functions.
generate_groupings() was the perfect candidate. It was unlikely to encounter
a very large range of inputs, and was very expensive for long word lengths. The
functools package makes memoization trivial by supplying the
@lru_cache() decorator.
Memoizing generate_groupings() lead to a notable, though still not
satisfactory reduction in execution time:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
[...]
real 11m15.483s
user 10m54.553s
sys 0m17.083s
Still, that's not bad for a single decorator from the standard library!
Case 2: Being Clever
My optimizations so far had helped slightly with case 1, but the core problem,
the inefficiency of generate_groupings() hadn't been addressed, and big
individual words still took too long to process:
$ time ./stoichiograph.py nonrepresentationalisms
[...]
real 0m20.275s
user 0m20.220s
sys 0m0.037s
Laziness can yield a certain degree of success, but sometimes cleverness is needed.
Recursion and the DAG
One evening as I was dosing off, I had a flash of inspiration and ran to my whiteboard to draw this:
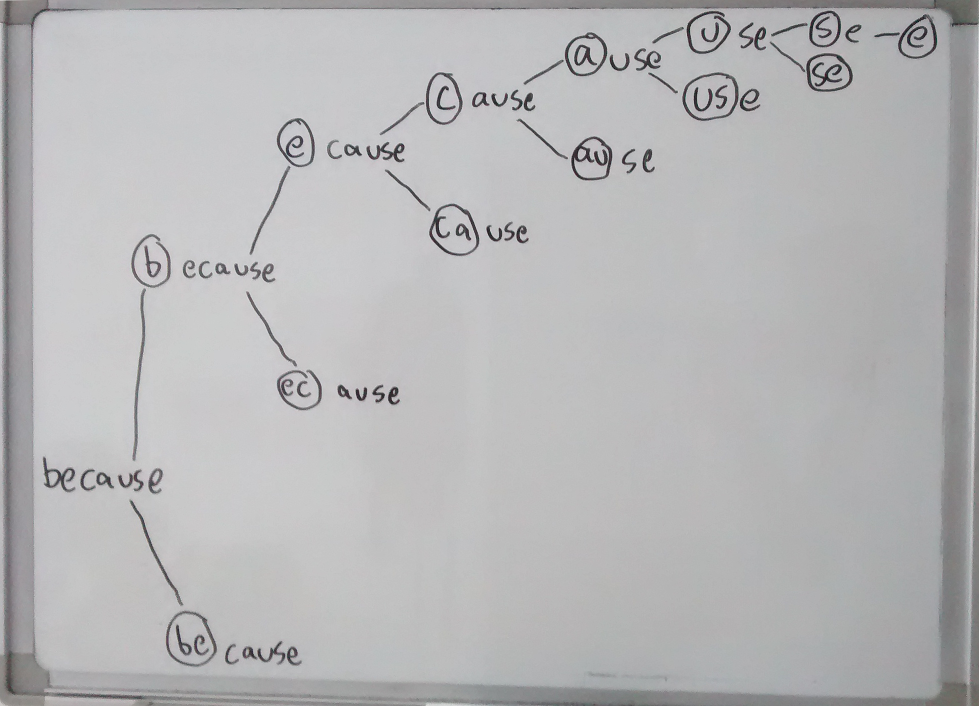
I realized I can take any string, pop the 1 and 2-character glyphs off the front, then recurse into the remaining substring in both cases. Once I've traversed the whole string, I will have found all the glyphs, and, critically, I will have information about their structure and order. I also realized that a graph could be a very good way to store this information.
So if the series of recursive function calls into our charming example word, 'amputation', looks something like this:
'a' 'mputation'
'm' 'putation'
'p' 'utation'
'u' 'tation'
't' 'ation'
'a' 'tion'
't' 'ion'
'i' 'on'
'o' 'n'
'n' ''
'on' ''
'io' 'n'
'ti' 'on'
'at' 'ion'
'ta' 'tion'
'ut' 'ation'
'pu' 'tation'
'mp' 'utation'
'am' 'putation'
Then, after filtering out all the glyphs that don't match any elemental symbol, we could end up with a nice graph like this:
Specifically, we will have made a directed acyclic graph (DAG) with each node holding a glyph. Each path from the first node to the last would be a valid elemental spelling of the original word!
I had never worked with graphs before, but I found a very helpful essay on the Python website that explained the basics, including how to efficiently find all paths between two nodes. The wonderful book 500 Lines or Less has a chapter with another example of a graph implementation in Python. I based my graph class on these examples.
With a simple graph class implemented and tested, I turned my whiteboard drawing into a function:
# A single node of the graph. A glyph and its position in the word.
Node = namedtuple('Node', ['value', 'position'])
def build_spelling_graph(word, graph, symbols=ELEMENTS):
"""Given a word and a graph, find all single and double-character
glyphs in the word. Add them to the graph only if they are present
within the given set of allowed symbols.
"""
def pop_root(remaining, position=0, previous_root=None):
if remaining == '':
graph.add_edge(previous_root, None)
return
single_root = Node(remaining[0], position)
if single_root.value.capitalize() in symbols:
graph.add_edge(previous_root, single_root)
if remaining not in processed:
pop_root(
remaining[1:], position + 1, previous_root=single_root
)
if len(remaining) >= 2:
double_root = Node(remaining[0:2], position)
if double_root.value.capitalize() in symbols:
graph.add_edge(previous_root, double_root)
if remaining not in processed:
pop_root(
remaining[2:], position + 2, previous_root=double_root
)
processed.add(remaining)
processed = set()
pop_root(word)
The Payoff
Where the initial brute-force algorithm operated horrifyingly in O(2^n) time,
this recursive one operates in O(n) time. Much better! The first time I timed my
newly optimized program on my word list file, I was blown away:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
[...]
real 0m11.299s
user 0m11.020s
sys 0m0.17ys
Execution time had gone from 16 minutes down to 10 seconds, the processing rate from 120 words per second to 10,800!
This was the first time I truly appreciated the power and value of data structures and algorithms.
The Actual Longest Word
With this newfound power I was able to find a new longest elementally spellable word: 'floccinaucinihilipilificatiousness.'
This amazing word comes from 'floccinaucinihilipilification,' defined as "the act or habit of describing or regarding something as unimportant, of having no value or being worthless," and often cited as the longest non-technical English word. 'Floccinaucinihilipilificatiousness' has 54 elemental spellings, all of which can experienced by any explorer brave enough to traverse its beautiful graph:
Time Well Spent
One may be tempted to floccinaucinihilipilificate on this whole endeavor, but I found it both valuable and important. When I began this project, I was relatively inexperienced at programming, and had no idea how to even begin. Progress was slow, and it took a long time to arrive at a satisfactory solution (look at the commit history to see the large gaps where I took a break to work on other projects).
However, I learned a great deal along the way. This project introduced me to:
- Combinatorics
- Performance profiling
- Time complexity
- Memoization
- Recursion
- Graphs and trees
Understanding these concepts has helped me again and again. Recursion and trees have been particularly important for my n-body simulation project.
Finally, it feels good to have answered my own initial question. I no longer
have to wonder about elemental spellings because I now have a tool to find them
for me, and with a quick pip install stoichiograph, you can too.
Discussion
- Some nice people (and a few well-intentioned bots) have participated in a discussion of this article on r/programming.
- This article was featured on Episode #26 of the excellent weekly podcast, Python Bytes.
Further Reading
Matus Goljer wrote a follow-up article that explores the generation of character groupings with dynamic programming:
I drew much inspiration from Peter Norvig's elegant solutions to interesting problems:
Two informative articles about performance profiling in Python: